主页
+Wiki
| 指标 | 平均 | 最差 |
|---|---|---|
| 空间 | \(O(n)\) | \(O(n)\) |
| 搜索 | \(O(log n)\) | \(O(log n)\) |
| 插入 | \(O(log n)\) | \(O(log n)\) |
| 删除 | \(O(log n)\) | \(O(log n)\) |
2-3树是一种3阶自平衡二叉搜索树,其每个内部节点有2个或3个子节点。外部节点没有子节点,有一个或两个数据元素。
插入
插入保持了树的平衡属性。
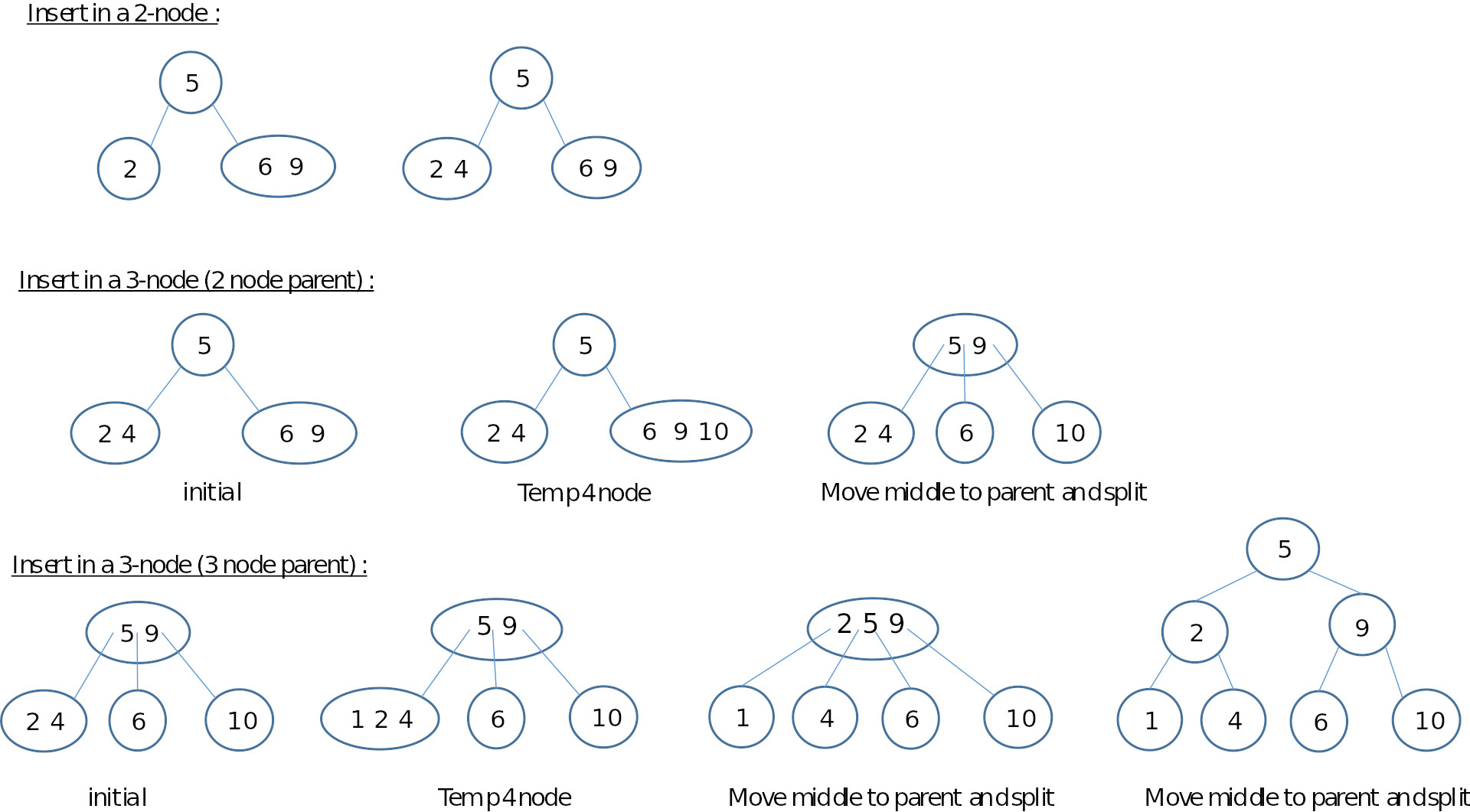
要插入到一个2节点中,新的键会以适当的顺序添加到2节点中。
要插入一个3节点,可能需要更多的工作,这取决于3节点的位置。如果树只由一个3节点组成,该节点将被分成三个2节点,并有适当的键和子节点。
如果目标节点是一个3节点,其父节点是一个2节点,那么键被插入到3节点中,以创建一个临时的4节点。在图中,键10被插入到有6和9的2节点中。中间的键是9,并被提升到父2节点中。这就留下了一个由6和10组成的3节点,它被分割为两个2节点,作为父3节点的子节点。
如果目标节点是一个3节点,而父节点是一个3节点,就会创建一个临时的4节点,然后如上所述进行分割。这个过程一直持续到树的根部。如果根必须被分割,那么就按照单个3节点的过程:一个临时的4节点根被分割成三个2节点,其中一个被认为是根。这个操作使树的高度增长了一个。
并行操作
由于2-3树在结构上与红黑树相似,红黑树的并行算法也可以应用于2-3树。